理论知识与问题特征
直接看理论枯燥无味,且印象不深,我们先从一些简单的例子开始,从而引出对应的知识点。
关于斐波拉契数列,大家应该很熟悉了,它的定义公示如下:
Fibonacci(n) = Fibonacci(n-1) + Fibonacci(n-2)
其中:Fibonacci(0) = 1,Fibonacci(1) = 1作为递归的经典入门例子,我们很快能想到它的递归解法:
func fibonacci(n int) int {
if n == 0 || n == 1 {
return 1
}
return fibonacci(n-1) + fibonacci(n-2)
}假设我们现在根据上面的递归代码要求出F(5)的值,按照递归铺开,可以得到下面这个计算过程:
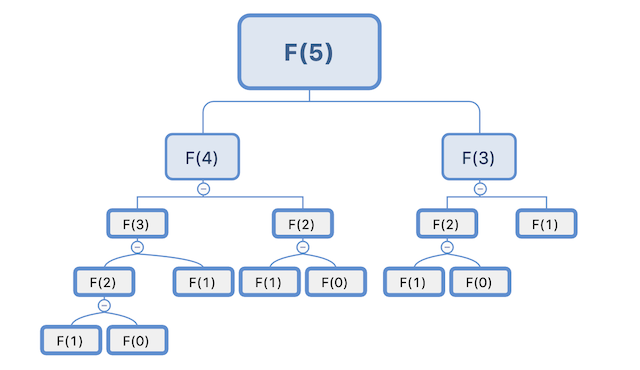
可以明显看到,里面有某些值是重复计算的,比如:F(2)就计算了3次。
我们可以对代码做一下优化:
func fibonacci(n int) int {
if n == 0 || n == 1 {
return 1
}
res := make([]int, n+1)
res[0] = 1
res[1] = 1
for i := 2; i <= n; i++ {
res[i] = res[i-1] + res[i-2]
}
return res[n]
}采用自底向上的方法,将过程中的计算结果保存起来,那么问题就变成了求解红色框框部分:
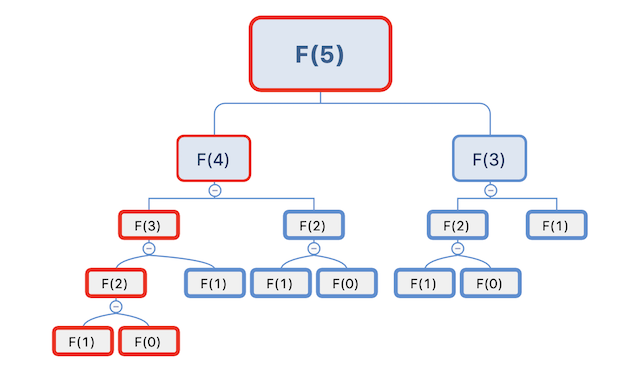
到了这里,我们引入了动态规划的其中一个特性:「重复子问题」 。重复子问题是指,问题的子问题之间是不独立的,一个子问题在后续阶段的决策中,可能会被多次用到。 利用这个特性,动态规划算法会将计算结果保存起来,避免子问题的重复计算。
那么问题到了这里就结束了吗,并不是,动态规划还有另外两个特性:最优子结构、无后效性,我们接下来就来分析它。
我们对斐波那契数列换一个描述:
有一条n格的楼梯在我们面前,我们一次可以走一格、或者走两格,请问,要到达第最顶端,我们可以有多少种爬法?
我们要到达第n格,可以有两种方式:
- 到达第(n-1)格后,走一格;
- 到达第(n-2)格后,走两格。
也就是说,到达第n格的方法等于到达第(n-1)格的方法加上到达第(n-2)格的方法。
f(n) = f(n-1) + f(n-2)
f(n-1) 和 f(n-2) 是 f(n) 的子问题,f(n) 的最优解可以从这两个子问题得到,因为这两个子问题本身也属于最优解,所以,我们称之为「最优子结构」。
f(n) 只需要知道 f(n-1) 和 f(n-2) 的值是多少,而并不关心它们究竟是怎么得到的,同时,一旦它们的值确定之后,不会受到后面的阶段影响,称之为「无后效性」。
总结
通过上面的简单例子,我们知道了动态规划的三个特性,动态规划能解决的有些问题复杂许多,我们留待后面的章节继续。
总结动态规划的三个特征:
- 重复子问题:不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态;
- 最优子结构:可以通过子问题的最优解,推导出问题的最优解;
- 无后效性:推导后面阶段状态时,只关心前面阶段状态的值,不关心是怎么得到的;某阶段状态一旦确定,不受后面阶段影响。